Quadratic Sieve

The idea

The idea behind the quadratic sieve is actually pretty simple.

If you have a relation of the form $ y^2 \equiv x^2\pmod n $ such that$ \ y \not\equiv x\pmod n $
it's easy to see that this implies$ n \vert (y^2 - x^2) $
which is the same as$ n \vert (y - x)(y + x) $
This tells us that$ \gcd(n, y - x) $ and$ \gcd(n, y + x) $are two factors of n.

The sieve polynomial

All we need to do is to find a relation of the given form. Actually we should find more than one because half the relations will yield the trivial factorisation. How to do this is due to an idea by Carl Pommerance back in '84. Take a look at the following polynomial:

$ \ f(x) = (x + \left\lfloor\sqrt{x}\right\rfloor)^2 - n $
We can see that the following relation is satisfied

$ \ f(x) \equiv (x + \left\lfloor\sqrt{x}\right\rfloor)^2\pmod n $
so the right side is already a square for any x.

Now consider a set of prime numbers $ p_1, p_2, ..., p_m $ called the factor base and assume that we have found two x values such that f(x) factors completely over the factor base. For example:

$ \ f(x_i) = p_1^2 * p_2^3 * p_7 $
$ \ f(x_j) = p_2 * p_7 * p_8^2 $

Neither of these values are square, but by multiplying them we get

$ \ f(x_i) * f(x_j) = p_1^2 * p_2^4 * p_7^2 * p_8^2 = (p_1 * p_2^2 * p_7 * p_8)^2 $
which clearly is a square.

Now we have two relations:

$ \ f(x_i) \equiv (x_i + \left\lfloor\sqrt{x_i}\right\rfloor)^2\pmod n $and$ \ f(x_j) \equiv (x_j + \left\lfloor\sqrt{x_j}\right\rfloor)^2\pmod n $

Multiplying them we get

$ \ f(x_i) * f(x_j) \equiv ((x_i + \left\lfloor\sqrt{x_i}\right\rfloor) * (x_j + \left\lfloor\sqrt{x_j}\right\rfloor))^2\pmod n $

which is a relation of the form we are looking for. This can of course be generalised to several values of x instead of just 2. We can now compute the gcd as described above and we have a factorisation of n. Computing the gcd can be done efficiently using the extended Euclidean algorithm.

Let's now take a look at how this can be done in practice.

Factor base

The requirements for the factor base are: As you can see 2 and 3 can't both be satisfied at the same time. The first requirement is not just satisfied by taking all the factor_base_size first primes starting from 2. If we have a prime p in our factor base we would like that for some i it is the case that

$ \ p \vert f(x_i) $

Inserting the value for f we see that

$ \ n \equiv (x_i + \left\lfloor\sqrt{x_i}\right\rfloor)^2\pmod p $

This means that n is a quadratic residue modulo p and hence our factor base should only consist of primes such that this is the case. Still, we should choose the primes as small as possible.

Sieving

The sieving step is the time consuming part of the algorithm where we try to find values of f(x) that factors completely over the factor base. Of course the trivial way of doing this (taking values of x as close to 0 as possible, compute f(x) and do trial division) is too slow, so we have to do a few tricks.

First we can show that

$ \ p \vert f(x) \Rightarrow p \vert f(x+kp) $

In order to obtain an initial solution (a value of x such that p|f(x) ) consider the following

$ \ f(x) \equiv 0\pmod p \Rightarrow (x + \left\lfloor\sqrt{x}\right\rfloor)^2 -... ...0\pmod p \Rightarrow (x + \left\lfloor\sqrt{x}\right\rfloor)^2 \equiv n\pmod p $

It is clear that this equation has at least two solutions and by what we have shown above, any solution will differ from one of these solutions by a multiple of p. These two solutions depend only on p and n so when we generate the factor base, we also compute and store them for each prime in the factor base.

An algorithm called the Shanks-Tonelli Algorithm can be used to compute these modular square roots efficiently.

Now we know enough to describe a somewhat efficient way of doing the sieving step.

First pick an interval close to 0 and compute log(f(x)) for each x in the interval.

Now loop over all primes in the factor base and for each x in the interval where p|f(x) we subtract log(p) from log(f(x))

We can do this efficiently because we already know all the values of x that satisfy this.

A value of f(x) that factors completely over the factor base should theoretically have it's 'log(f(x))' reduced to zero by this procedure (remember that log(f(x)) - log(p) = log(f(x)/p). However this is not always the case because

But if we specify a reasonable threshold and only consider values of f(x) where our initial log(f(x)) have been reduced below that threshold, we have eliminated a lot of candidates that would never have factored over the factor base. We can now do trial division on the rest. The size of the threshold is a trade-off between throwing away too many good solutions and spending too much time doing trial division. When we find a value of x such that f(x) factors completely over the factor base we store x in an array and the prime factors of f(x) in a matrix.

The matrix is in GF(2) and has factor_base_size columns and factor_base_size + 10 rows (will be explained in the next section). Each row corresponds to one value of f(x) and the column i contains a 1 if the i'th element of the factor base was a factor of f(x) occurring an odd number of times and a 0 if it occurred an even number of times.

The sieving step ends when we have filled the matrix. If that does not happen in the chosen interval we will just pick another and repeat the sieving step. However, if the factor base was too large or too small we might have to wait a very long time for the matrix to be filled because the values of f(x) become larger and hence more unlikely to factor over the factor base.

Gaussian elimination

Let's call our matrix from the sieving step A. We want to pick a subset of the rows of A such that the sum of their columns modulo 2 is the zero vector, because that means if we multiply the f(x) values corresponding to these columns we get a square (recall the example from the beginning of this section).

If we call the i'th row of A$ \hat{a_i} $ and$ e_i $ is either 0 or 1, then what I have just written above is actually that we want to choose values of$ e_i $ such that$ \ \hat{a_1}e_1 + \hat{a_2}e_2 + ... + \hat{a_k}e_k \equiv 0\pmod 2 $

This means that we have to solve

$ \ \hat{e}A = \hat{0}\pmod 2 $
where

$ \hat{e} = (e_1, e_2, ..., e_k) $
Once we have this solution the$ e_i $'s that are 1 will tell us which f(x) values to multiply to get a relation of the form we are looking for.

This can be solved by augmenting A with the identity matrix I and performing Gaussian elimination on the augmented matrix. After the Gaussian elimination we can read the e vector as a row in I next to a 0 row in A (this is probably not obvious, but don't worry about that).

There are more efficient ways of solving this since we can take advantage of the fact that the matrix is a sparse matrix in GF(2) with most non-zero entries to the left.

Once we have the solutions we multiply them and use the extended Euclidean algorithm to compute the gcd as described in the beginning, obtaining a factorisation of n.

Because our original matrix had 10 more rows than columns we have at least 10 different solutions which is good because for each solution there is a fifty-fifty chance that it will yield the trivial factorisation of n.

The multiple polynomial variation

A problem with the version we have just seen is that once x gets large f(x) gets large and it becomes difficult to find values of f(x) that factors completely over the factor base. This is where the multiple polynomial quadratic sieve (MPQS) enters the arena. As the name implies this version uses several polynomials in order to keep the values of f(x) small. Not only does this make the values of f(x) smaller, but it also enables us to use a smaller sieve interval and a smaller factor base. Of course all this is done to decrease the running time of the algorithm.

There are several variations of this algorithm. Here I will just present one of them.

The polynomials

Let's look at polynomials of the form$ \ f(x) = Ax^2 + 2Bx + C $
Let A be a square and choose$ \ 0 \leq B < A $ such that$ \ B^2 \equiv n\pmod A $
This can only be done if n is a square modulo q for every prime q that divides A, so we must at least choose A with a known factorisation.

Finally we choose C such that$ \ B^2 - AC = n $
This is possible due to our choice of B. Now look what happens when we multiply f(x) by A:

$ \ A \cdot f(x) = (Ax)^2 + 2ABx + AC = (Ax)^2 + 2ABx + B^2 - n = (Ax + B)^2 - n \Rightarrow (Ax + B)^2 \equiv A \cdot f(x)\pmod n $
If we look closely at the relation above we see that we can use this new f(x) just as we did before. The crucial point here is that even if we multiply values of f(x) obtained with different values of A, B and C we still get a relation of the form we are looking for. So when one polynomial gets too large we discard it and choose a new one. This is why this is called the multiple polynomial version.

The math behind it

So how should we choose A? Well, we need to minimise the value of f(x) over the sieving interval [-M, M]. One way to do this is to have the minimum and maximum value of f(x) over [-M, M] be of the same magnitude but of opposite sign. It's easy to see that f(x) has a minimum where$ \ x = \frac{-B}{A} $. Because of our choice of A and B we know that$ \ -1 < \frac{-B}{A} \leq 0 $, or in other words that our minimum is close to 0. Evaluating f(x) in that point we get$ \ f(\frac{-B}{A}) = \frac{-n}{A} $

Then our maximum must be in -M or M and it will roughly be of size$ \ \frac{(A^2M^2 - n)}{A} $. We want this to be as close to$ \ \frac{n}{A} $ as possible so we choose$ \ A = \frac{\sqrt{2n}}{M} $
To help us select a suitable A choose a prime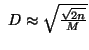$ \ D \approx \sqrt{\frac{\sqrt{2n}}{M}} $such that n is a square modulo D and$ \ D = 3\pmod 4 $.
Set$ \ A = D^2 $. A is now close to the value we wanted and we also know that n is a square modulo q for every prime q that divides A.

Now we need to find B. Consider the following values and keep in mind that$ \ D = 3\pmod 4 $

$ h_0 \equiv n^{\frac{D-3}{4}}\pmod D $

$ h_1 \equiv n^{\frac{D+1}{4}}\pmod D $

This gives us

$ h_1^2 \equiv n^{\frac{D+1}{2}} \equiv nn^{\frac{D-1}{2}}\pmod D \equiv n\pmod D $

Now define

$ h_2 \equiv (2h_1)^{-1}\left(\frac{n-h_1^2}{D}\right)\pmod D $

The inverse of$ 2h_1 $ always exists since we are in$ Z_D $ where D is a prime and can be computed efficiently using the extended Euclidean algorithm.

Now we can choose$ B \equiv h_1 + h_2D\pmod A $ which can be easily checked to satisfy$ B^2 \equiv n\pmod A $

Finally C can be chosen by solving$ B^2 - AC = n $ which will always have a solution due to the choice of B.

When we need a new polynomial we just choose the next D that satisfies the requirements and generate new values of A, B and C.

There are other things to consider. What about the factor base for example? We must of course keep the same factor base for all polynomials so is the requirement that all primes in the factor base should be chosen such that n is a quadratic residue modulo each of them still valid? Remember that the reason for choosing the factor base this way, was that we only wanted primes where for at least one x it was the case that p | f(x). Recall that:

$ A \cdot f(x) = (Ax + B)^2 - n $

Let p be a prime in the factor base:

$ p \vert A \cdot f(x) \Rightarrow p \vert (Ax + B)^2 - n \Rightarrow n \equiv (Ax + B)^2\pmod p $

So if we choose A such that there does not exist primes in the factor base that divides A this is equivalent to require that for each prime p in the factor base, n is a quadratic residue modulo p. Hence we only have a problem if a prime in the factor base is equal to D. Note that even if this happens the only harm done is that we will have one element in the factor base that never divides f(x).

Bottom line is that we choose the factor base just as before.

Just as before we need to solve f(x) = 0 (mod p) for each prime in the factor base, but this time we need to do it each time we generate a new polynomial. This is easy to do using the standard formula for solving a polynomial of 2nd degree.

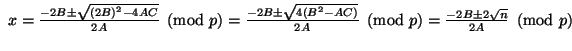
$ \ x = \frac{-2B \pm \sqrt{(2B)^2 - 4AC}}{2A}\pmod p = \frac{-2B \pm \sqrt{4(B^2 - AC)}}{2A}\pmod p = \frac{-2B \pm 2\sqrt{n}}{2A}\pmod p $
$ \ \sqrt{n}\pmod p $ can be computed using the Shanks-Tonelli algorithm and the inverse of 2A can always be found since we are in$ Z_p $where p is a prime. Of course$ \ 2\sqrt{n}\pmod p $ can be precomputed for each prime in the factor base.

The rest of the algorithm works exactly the same way as in the single polynomial case, except for the fact that we don't keep sieving until we have enough relations, but instead choose a new polynomial and restart the sieving once f(x) gets too large.

Optimisations

What I have described so far is a simple version of the algorithm. There are several possible optimisations and I will briefly sketch some of them here.

A simple optimisation is the Small Prime Variation. The idea is that small primes doesn't contribute much to the sieving so we might as well stop wasting our time on them. Of course we have to adjust the sieving threshold a little.

Another related optimisation is the Large Prime Variation. Here the idea is that even though a number doesn't fully factor over the factor base we can still use that number. If we can factor the number over the factor base with a remainder that is one large prime, we store the number and the large prime. If we later find a number that factors completely except for the same large prime we can now use these two numbers since the result will still be a square if it includes these two numbers. The name can be a bit misleading since the "large prime" doesn't have to be a prime at all. Still we need some criteria for the numbers to keep or else we will quickly run out of memory, requiring that these extra numbers are primes are one way to increase the chance that we will find two f(x) values with the same large prime as a factor. Of course this method can be extended to two large primes instead of only one at the cost of more memory usage.

A very useful optimisation regarding a parallel implementation of the multiple polynomial version is to choose A different from what I described above. If we choose A to be a product of k primes not in the factor base we can find$ \ 2^{k-1} $ values of B that can be used for each A, that is they satisfy$ \ B^2 \equiv n\pmod A $. This allows the server to choose a value of A and send it to the client. The client can now compute several polynomials on it's own without having to communicate with the server. This would be very useful for a distributed factoring algorithm over the internet.

Performance

It is very hard to give an exact running time for the quadratic sieve, but it depends mostly on the length of the sieving interval, the size of the factor base and the threshold value that decides when to do trial division on a number. Check the literature section for a paper that gives a detailed analysis of the running time of the quadratic sieve since that is a whole project in itself.

I have found "optimal" values in the literature for the relation between the size of the factor base and the sieving interval, but the literature is also full of empirical results that do not match the theoretic optimal values. Basically what you do if you want to factor a large number is that you do a lot of analysis of that number and generate special polynomials. Also for some values of n it's better to factor a multiple of n instead since that would suit the selected polynomial better. Of course if you really want to factor large numbers today you would probably not use the quadratic sieve, but the number field sieve instead which is faster for really large numbers (more that 130 digits or so). If you want to factor small primes (less than 13 digits or so) there are methods that are a lot faster than the quadratic sieve.

I'll end this section with running times for the quadratic sieve and the number field sieve given the theoretical optimal values. These numbers are taken from "Stinson: Cryptography - Theory and Practice".

Quadratic sieve: $ O\left(e^{\left(1 + O(1)\right)\sqrt{\ln n \ln \ln n}}\right) $
Number field sieve: $ \ O\left(e^{\left(1.92+O(1)\right)(\ln n)^{\frac{1}{3}}(\ln \ln n)^{\frac{2}{3}}}\right) $